1. Backgrounds
Recommender system
정보가 넘쳐나는 현 시대에서 추천 시스템은 전자 상거래, 온라인 뉴스 및 소셜 미디어 사이트를 포함한 많은 온라인 서비스에 널리 채택되어 정보 과부하를 완화하는 데 중요한 역할을 하고 있습니다.
컨텐츠 기반(content-based) 방법과 더불어 추천시스템의 한가지 큰 줄기인 협업 필터링(Collaborative Filtering)은 특정 아이템에 대한 유저의 선호도를 평점과 방문기록 등의 과거 상호관계(interaction)에 기반하여 모델링합니다.
Matrix factorization

협업 필터링에서 가장 대중적으로 사용되는 기술은 Matrix Factorization 입니다. 'Netflix Prize'를 통하여 유명해진 Matrix factorization은 latent space를 공유하는 User vector와 Item vector의 내적을 통해 Interation을 모델링하는 방법입니다.
SVD(singular vector decomposition)와 궤를 같이 한다고 생각하시면 좋을 것 같습니다.
\(p_u\),\(p_i\)를 각각 User, Item의 latent vector로 하였을때 interaction \(\hat{y}_{ui}\)는 다음과 같이 계산됩니다.
$$\hat{y}_{ui} = f(u,i|p_u,q_i) = {p_u}^Tq_i = \sum_{k=1}^K p_{uk}q_{ik}$$
MF는 또한 User, Item 간의 Sparse한 Interaction Matrix를 채워주는 Matrix completion이라고도 할 수 있습니다.
MF(Matrix Factorization)의 매우 효율적이며 뛰어난 성능 앞에서, 당시에는 MF 방법론을 개선하기 위한 연구들이 주로 진행되고 있었습니다.
하지만 MF는 명확한 한계점이 존재합니다.
MF가 Interaction을 모델링 하기 위해 사용하는 내적(inner-product)은 latent feature를 선형적으로 곱하는 단순한 방법으로 매우 효율적 이지만, 이는 동시에 내적이 선형적인 관계만을 모델링할 수 있음을 의미하고 있습니다.
MF의 표현적 한계점을 아래의 예시를 통해 자세히 설명드리도록 하겠습니다.
다음의 User-item 행렬은 User 1~4와 Item 1~5의 상호관계를 나타내고 있습니다.
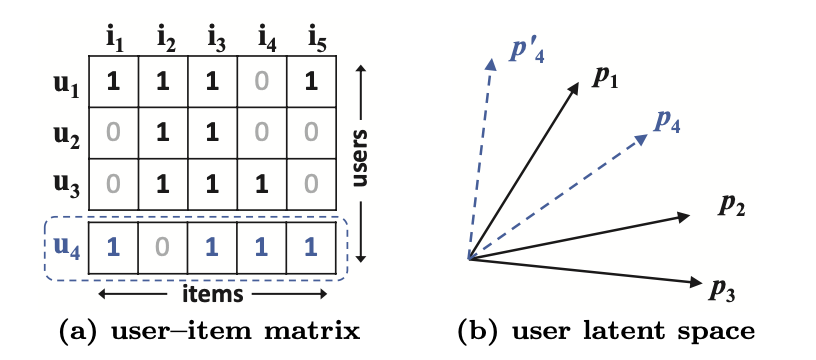
이러한 경우 MF는 user와 item을 같은 latent space에 위치시키기 때문에, user 사이의 유사도 또한 내적으로 나타낼 수 있습니다.
또한 latent vector가 단위 벡터라는 가정 하에는 코사인 유사도 등의 방법도 가능해 집니다.
따라서 간단하게 (a)의 user-item matrix에서 자카드 유사도를 고려하는 경우를 가정해 보겠습니다.
$$s_{ij} = {|R_i|\cap|R_j| \over |R_i|\cup|R_j|}$$
\( u_1,u_2,u_3 \)에 대해서 다음의 자카드 유사도 대소관계가 성립합니다.
$$ s_{23}(0.66) > s_{12}(0.5) > s_{13}(0.4) $$
이러한 대소관계를 이용하여 \( u_1,u_2,u_3 \)를 latent space에 각각 \(p_1,p_2,p_3\)로 나타낸다면 (b)와 같을 것 입니다.
이제 여기에 \(u_4\)를 추가하여 고려해 보겠습니다. \(u_4\)는 나머지 \( u_1,u_2,u_3 \)와 다음의 유사도 대소관계를 갖습니다.
$$ s_{41}(0.6) > s_{43}(0.4) > s_{42}(0.2) $$
이제 \(u_4\) 또한 (b)의 latent space에 \(p_4\)로 나타내어 보겠습니다.
\(u_4\)는 \(u_1\)과 가장 유사합니다. 따라서 \(p_4\)를 위해서는 점선으로 표현되는 두가지 위치 \(p_4',p_4\)가 가능합니다.
무엇인가 잘못되었음을 느끼실 것입니다. 두가지 경우 모두 \(p_4\)는 \(p_3\)보다 \(p_2\)에 가깝게 위치됩니다.
\( s_{41}(0.6) > s_{43}(0.4) > s_{42}(0.2)\)의 유사도 관계를 표현할 수 없는 상황이 되어버린 것 입니다.
다음의 문제를 MF에서는 어떻게 해결할 수 있을까요??
더 높은 차원의 latent space를 도입한다면(하나의 축을 추가한다면) 더 복잡한 대소관계 표현이 가능해 질 것입니다.
하지만 latent space의 차원을 증가시키는 것은 잘 아시다시피 모델의 일반화 성능(generalization)을 저해할 수 있는 방법입니다.
따라서 내적은 User와 Item 사이의 복잡한 비 선형적 상호관계를 모델링 하기에는 불충분할 수 있습니다.
협업 필터링을 위한 MF 방법론의 자세한 설명은 아래 리뷰를 참고 부탁드립니다.
[paper review][추천시스템]Matrix Factorization Techniques for recommender systems
Recommender System 정보가 넘쳐나는 현 시대에서 추천 시스템은 전자 상거래, 온라인 뉴스 및 소셜 미디어 사이트를 포함한 많은 온라인 서비스에 널리 채택되어 기호에 맞는 상품을 제공하고 있습
supkoon.tistory.com
이러한 선형적, 비선형적 표현의 관점에서 문제를 생각한다면,
비 선형적인 관계를 모델링할 수 있는 대표적인 방법은 심층신경망(Deep Neural Network) 입니다.
기존의 연구들 중에서도 심층신경망을 협업필터링에 적용하기 위한 시도들이 있었습니다. 하지만, 대부분의 심층신경망은 음성, 문자, 이미지 등의 부가적인 특징을 모델링하기 위해서만 쓰여왔습니다.
본 논문은 심층신경망을 사용하여 데이터 사이의 상호관계를 직접 모델링하기 위한 연구내용을 담고 있습니다.
Kind of Interactions : explicit? implict?
협업 필터링은 앞서 말씀드린 내용과 같이, 과거의 모든 상호작용들을 바탕으로 새로운 데이터에 대한 개인화된 상호작용을 예측하여 주는 추천시스템 입니다.
우선, 협업필터링을 위해 사용되는 데이터에는 두가지 종류가 존재합니다.
1) Explicit feedback
Item에 대한 User의 모든 직접적인 평가를 포함하는 데이터 입니다.
구하기는 어렵지만 바로 사용해도 좋을만큼 데이터의 품질이 좋은 경우가 많습니다.
ex) 평점, 취향, 후기, ...
2) Implicit feedback
직접적으로 Item과 User간의 선호 관계를 나타내지는 않지만, 간접적인 정보를 포함하고 있는 데이터 입니다.
다양한 방법을 통하여 구할 수 있지만, 의미를 파악하기는 어렵습니다.
ex) 방문기록, 검색기록, 구매여부, 장바구니, ....
본 논문에서는 Implicit feedback을 활용하여 신경망을 학습합니다.
Implicit feedback은 관계 파악이 어렵지만, 많은 양의 데이터를 구할 수 있기 때문에 신경망 구조의 유효성을 검증하기에 알맞다고 할 수 있습니다.
Implicit feedback에 의해 본 논문의 User u와 item j간의 interaction인 \(y_{ui}\)는 다음과 같이 binary로 표현됩니다.

\(y_{ui}\)가 1이라는 것은 Implicit feedback으로 부터 u와 i 사이의 관계가 관찰되었음을 의미하며, 특별히 선호도를 나타내지는 않습니다. 따라서 NCF가 학습하는 문제는 User와 item 사이의 interaction 유무를 예측하는 binary classification이 됩니다.
본 논문의 세가지 주된 Contribution은 다음과 같습니다.
1) User와 Item 사이의 latent feature를 모델링하기 위한 신경망 기반의 general framework인 NCF를 제안합니다.
2) MF 역시 NCF의 한가지 종류임을 증명하고, 비 선형적인 관계를 모델링하기 위해 NCF를 사용합니다.
3) 현실의 데이터셋을 통해 검증하여 NCF의 효율성을 증명합니다.
2. Neural Collaborative Filtering
General Framework

NCF는 간단하게 4개의 layer로 구성됩니다.
사실 신경망 모델에 관한 어느정도의 지식을 갖고계신 분이라면, NCF는 너무나도 당연하며, 간단한 구조일 수 있습니다.
하지만 본 논문은 특정한 모델의 specification 보다도, 신경망을 사용하는 협업필터링의 General Framework를 제안하고 있습니다.
1)Input Layer(sparse)

Input Layer는 각각 user, item을 나타내는 feature vector \(v_u^U\)와 \(v_i^I\)로 구성됩니다.
각각의 벡터는 one-hot encoding으로 표현되어 매우 sparse한 상태입니다.
2)Embedding Layer

Embedding layer는 sparse한 input vector를 Dense하게 바꿔주는 역할을 합니다.
일반적인 임베딩 방법과 동일하게 fully-connected layer가 사용됩니다.
Embedding Matrix를 통하여 M,N 차원의 user,item vector를 K차원의 latent space에 표현한 것으로도 생각해 볼 수 있습니다.
User latent Vector는 Embedding Matrix \(P \in \mathbb{R}^{M\times K}\)에 대해 \(P^Tv_u^U\)로 표현되며,
Item latent Vector는 Embedding Matrix \(Q \in \mathbb{R}^{N\times K}\)에 대해 \(Q^Tv_i^I\)로 표현됩니다.
3)Neural CF Layers

임베딩이 완료된 User, Item latent vector는 여러 층의 신경망을 거치게 됩니다.
이 다층 신경망 구조를 Neural CF Layers라고 합니다.
우선 User latent vector와 Item latent vector를 concatenate한 벡터를 시작으로
각각의 층을 거치며 인공신경망을 통해 복잡한 비선형의 데이터 관계를 학습할 수 있게 됩니다.
4)Output Layer

마지막 Layer인 Output layer에서는 NCF layer의 hidden vector를 input으로 받아 predictive score \(\hat{y}_{ui}\)를 예측하며, Target \(y_{ui}\)와의 비교를 통해 학습이 진행됩니다.
이러한 NCF 모델을 다음과 같은 수식으로 간단하게 나타내 볼 수 있습니다.
$$\hat{y}_{ui} = f(P^Tv_u^U,Q^Tv_i^I|P,Q,\theta_f)$$
\(P\)와 \(Q\)는 앞서 설명드린 embedding layer의 Matrix \(P \in \mathbb{R}^{M\times K}\), \(Q \in \mathbb{R}^{N\times K}\)이며, \(\theta_f\)는 interaction function \(f\)의 모델 파라미터를 의미합니다.
이때 우리는 model \(f\)를 multi-layer neural network로 정의하였기 때문에, 다시 아래와 같이 표현할 수 있습니다.
$$f(P^Tv_u^U,Q^Tv_i^I) = \phi_{out}(\phi_X(...\phi_2(\phi_1(P^Tv_u^U,Q^Tv_i^I))...))$$
Training
$$L_{sqr} = \sum_{(u,i)\in y\cup y^-} w_{ui}(y_ui-\hat{y}_{ui})^2$$
데이터들이 Gaussian distribution에서 왔다는 가정 하에 위와 같은 Squared loss를 설정할 수도 있습니다.
하지만 NCF는 binary 형태의 implicit data를 사용하여 학습하는 구조이기 때문에, 자연스럽게 bernoulli distribution을 가정하였습니다. bernoulli distribution가정에 따른 likelihood는 다음과 같습니다.
$$p(y,y^-|P,Q,\theta_f) = \prod_{(u,i)\in y}\hat{y}_{ui} \prod_{(u,j)\in y^-}(1-\hat{y}_{uj})$$
따라서 목적함수로 사용하기 위한 Negative log likelihood의 형태는 다음과 같이 표현됩니다.
$$L = -\sum_{(u,i)\in y}log\hat{y}_{ui} - \sum_{(u,j)\in y^-}log(1-\hat{y}_{uj})$$
$$=- \sum_{(u,i)\in y\cup y^-} y_{ui}log\hat{y}_{ui}+(1-y_{ui})log(1-\hat{y}_{ui})$$
Optimizer로는 SGD가 사용됩니다.
2.Generalized Matrix Factorization(GMF)
저자들은 MF(matrix factorization)역시 NCF framework의 특수한 경우로 해석될 수 있음을 보여줍니다.
우선 latent vecter \(P^Tv_u^U\),\(Q^Tv_i^I\)를 각각 \(p_u\),\(q_i\)라고 했을 때, 첫번째 NCF layer의 mapping function을 다음과 같이 표현해 보겠습니다.
$$\phi_1(p_u,q_i) = p_u\odot q_i$$
그다음 결과를 output layer에 project한다면 아래와 같이 표현 될 수 있습니다. \(a_{out}\)는 activation function을 의미하며, \(h\)는 output layer의 가중치를 의미합니다.
$$\hat{y}_{ui} = a_{out}(h^T(p_u \odot q_i))$$
이 때, \(\odot\)를 element-wise product로, \(a_{out}\)을 identical function(항등함수)로, h를 [1,1,1,....] 형태의 uniform vector로 가정한다면,
이 조건에서의 NCF framework는 Matrix Factorization과 동일해집니다. 따라서 NCF의 framework에서 MF는 쉽게 일반화와 확장이 가능합니다.
Generalized Matrix Factorization(GMF)란 NCF framework에서 MF를 일반화, 확장한 한가지 형태 입니다.
GMF에서 저자들은 \(a_{out} = \sigma(x) = 1/(1+e^{-x})\)로 지정하고, h를 학습 가능한 non-uniform weight로 지정하여 latent feature 사이의 중요도를 고려할 수 있도록 하였습니다.
3.Multi-Layer Perceptron(MLP)
MLP역시 NCF framework의 특별한 형태로 표현할 수 있습니다.
$$z_1 = \phi_1(p_u,q_i) = \begin{bmatrix}p_u\\q_i\end{bmatrix}$$
$$\phi_2(z_1) = a_2(W_2^Tz_1+b_2)$$
$$.....$$
$$\phi_L(z_{L-1}) = a_L(W_L^Tz_{L-1}+b_L)$$
$$\hat{y}_ui = \sigma(h^T\phi_L(Z_{L-1}))$$
우선 \(\phi_1\)은 concatenate 함수입니다.
그리고 각각 \(W_x,b_x,a_x\)는 x번째 layer의 Weight matrix, bias vector, activation function을 의미합니다.
MLP에 대한 activation function은 일반적으로 사용하는 신경망의 activation function 중 자유롭게 선택이 가능합니다.
MLP는 GMF에 비해 여러 층의 신경망을 사용하여 더욱 비 선형적이며 복잡한 관계를 학습할 수 있습니다.
4.Fusion of GMF and MLP

저자들은 최종적으로 NCF의 두가지 예시인 GMF와 MLP를 융합한 모델을 제안합니다.
$$\phi^{GMF} = p_{u}^{G} \odot q_{i}^{G}$$
$$\phi^{MLP} = a_{L}(W_{L}^{T}(a_{L-1}(...a_{2}(W_{2}^{T} \begin{bmatrix} p_{u}^{M} \\ q_{i}^{M} \end{bmatrix}+b_{2})...))+b_{L})$$
$$\hat{y}_{u,i} = \sigma(h^{T} \begin{bmatrix}\phi^{GMF} \\ \phi^{MLP} \end{bmatrix})$$
이 때, \(p_u^G, q_i^G\)는 GMF를 위한 embedding Matrix이며,
\(p_u^M, q_i^M\)은 MLP를 위한 embedding Matrix로 서로 다른 차원의 임베딩을 가질 수 있습니다. 또한 각각 학습이 가능합니다.
최종 score는 MLP와 GMF의 output을 concatenate하여 사용합니다.

MF와 MLP는 각각의 장단점이 존재합니다.
추천시스템에 있어서 선형관계를 포착하는 MF가 아직도 사용되는 이유 또한 선형관계의 중요성에 있습니다.
제안된 fusion 모델은 선형, 비선형의 Interaction을 모두 포착할 수 있는 모델 입니다.
저자들은 이 모델을 Neural Matrix Factorization이라고 이름 지었습니다.
5.Results
검증과정은 다음의 두가지 데이터셋으로 진행되었습니다.
MovieLens, Pinterest 모두 현실의 문제를 다루고 있는 데이터셋입니다.

Pinterest의 경우 데이터셋이 매우 크지만 상대적으로 조금 더 sparse 합니다.
result 1.

HR@10은 10개 중에 몇개를 맞추었는지(hit)를 의미하는 지표입니다.
NDCG는 랭킹 추천에 많이 쓰이는 지표로, 이상적인 정답 랭킹과 예측 랭킹을 비교하는 지표입니다.
첫번째 행의 그래프들을 통해 제안한 방법인 NeuMF가 기존의 Baseline을 크게 웃도는 성능을 보여주었음을 확인할 수 있습니다.
두번째 행은 1에서 10까지의 K에 따른 HR@K를 비교한 결과입니다. K의 증가에 따라서도 NeuMF의 성능이 가장 우수함을 확인할 수 있습니다.
result 2.
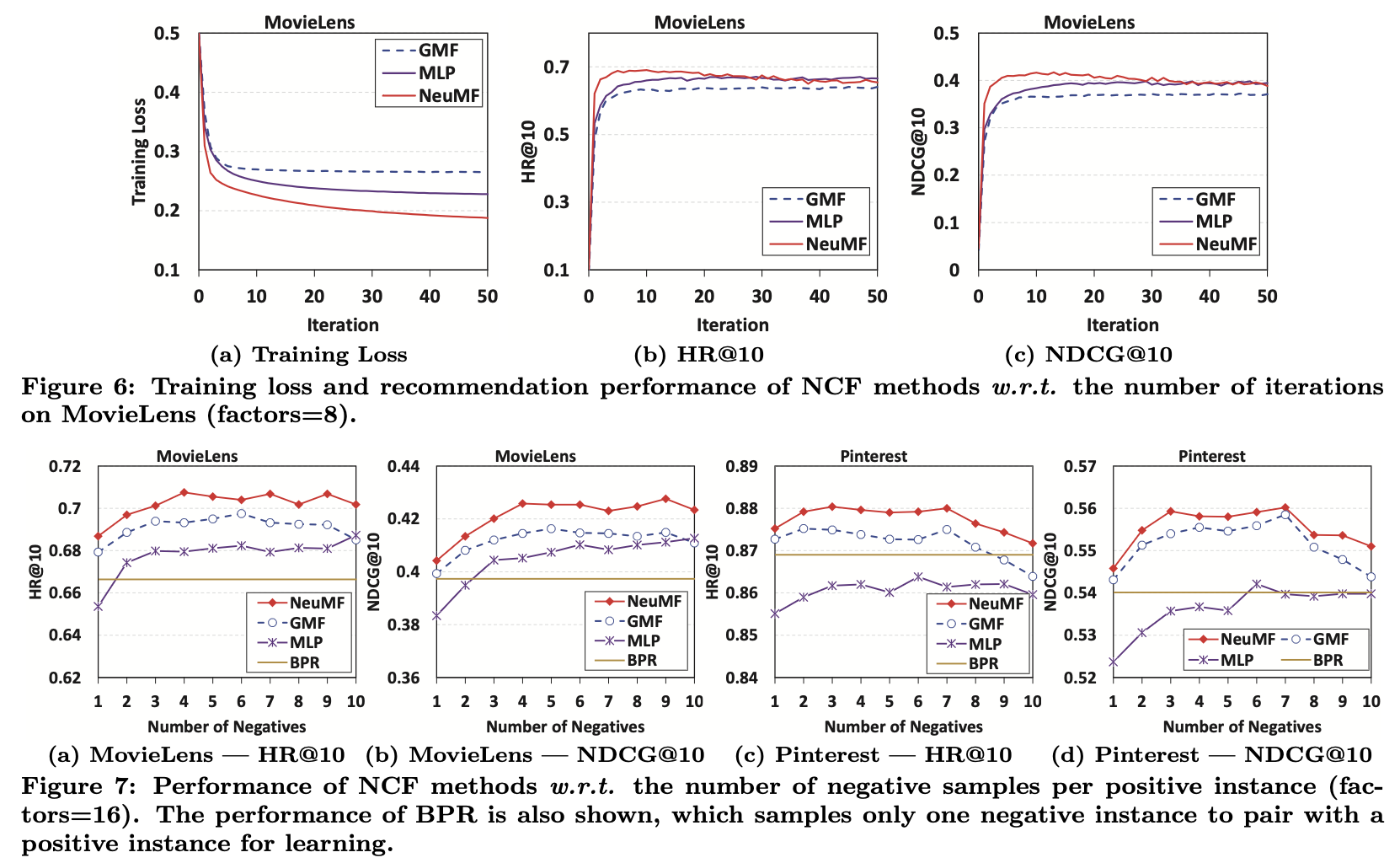
첫번째 행의 결과를 통해 학습을 거듭할 수록 지속적으로 성능이 증가했음을 알 수 있습니다. 또한 세가지 NCF 방법 중에서 fusion 버전인 NeuMF가 가장 낮은 training loss를 달성하였습니다. (NeuMF > MLP > GMF)
두번째 행은 log loss 계산에 있어서 Negative sample의 수에 따른 결과 비교입니다.
Negative sampling을 진행하였을 시에도 NeuMF의 성능이 가장 좋았으며, 너무 작거나 6이상의 샘플링을 진행한 경우에는 오히려 성능이 하락하였습니다. 따라서 최적의 sampling ratio는 3~6임을 알 수 있습니다.
result 3.

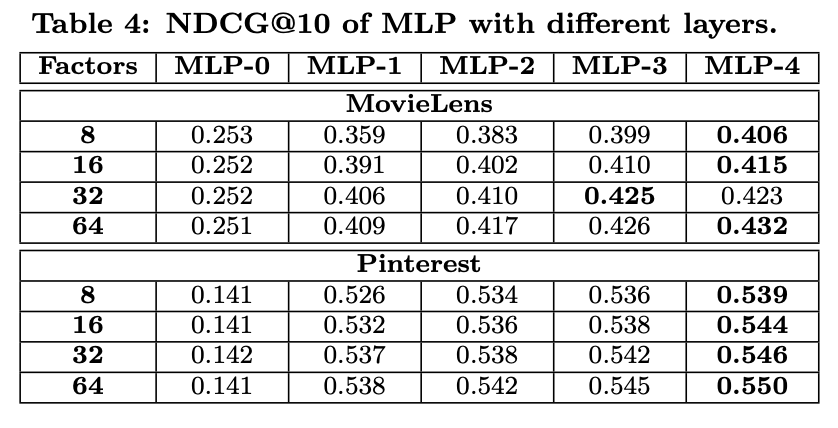
마지막 실험은 "과연 딥러닝(neural network)이 정말 추천시스템에 도움이 되는가?" 라는 질문에 대한 검증입니다.
MLP-0은 hidden layer가 없는 구조를 의미합니다.
Layer의 수와 latent factor의 증가에 따라서 성능이 거의 일관되게 증가하는 것을 확인할 수 있으며, 따라서 NCF가 효용성이 있는 구조임을 입증하였습니다.
6.구현
추천시스템을 공부하며 실전감각을 기르기 위해 구현을 함께 진행하였습니다.
Movielens를 바탕으로 논문에 기술되어 있는 내용을 그대로 구현하였습니다.
성능에는 크게 초점을 두고 있지 않기 때문에 이점 양해 부탁드립니다.
supkoon/neuralCF_tf2
Contribute to supkoon/neuralCF_tf2 development by creating an account on GitHub.
github.com
마무리
추천시스템은 현재 머신러닝이 가장 크게 개입하고 있는 분야 중 하나라고 생각합니다.
본 논문의 NCF는 신경망을 사용하는 general한 협업필터링 framework 로서, 간단하게 다양한 모델들을 표현할 수 있었습니다.
또한 저자들은 NCF로 구성한 MF의 일반화 형태인 GMF와 MLP를 융합하여 NeuCF를 제안하였으며, 기존의 모델에 비해 우수한 성능을 달성하였습니다.
추천시스템에 있어서는 선형, 비선형 모델이 모두 중요하게 고려됩니다. NeuCF도 같은 흐름에서 장점을 갖고있는 모델이라고 생각합니다.
추천시스템에 대해 전반적으로 공부를 진행하던 중에 논문을 읽게되어 본 리뷰를 작성하였습니다. 오랜만에 논문을 직접 구현해보느라 미숙했던 점도 많지만 배우는 부분이 많았던 것 같습니다.
다음 시간에는 같은 추천시스템 논문인 Factorization machine에 대한 리뷰, 구현을 진행해보도록 하겠습니다.