DNN

DNN(deep neural network)은 비선형구조와 병렬계산을 통하여 다양한 분야에서 SOTA를 달성하기 시작하였습니다.
하지만 고정된 차원의 input과 output을 필요로 하는 일반적인 DNN의 구조는 길이가 고정되지 않은 입, 출력을 필요로 하는 실제 문제들에 DNN을 적용하는데 있어 제약으로 작용하였습니다.
RNN
RNN은 시퀀스를 처리할 수 있는 DNN의 generalization version 입니다.
RNN은 입력 시퀀스 \((x_1,...,x_T)\)를 출력 시퀀스 \((y_1,...,y_T)\)로 매핑할 수 있습니다.
$$h_t = sigmoid(W^{h\mathbf{x}}x_t + W^{hh}h_{t-1})$$
$$y_t = W^{\mathbf{y}h}h_t$$
Timestep \(t\)에서 RNN은 입력 \(x_t\)와 이전 timestep의 hidden state \(h_{t-1}\)을 함께 고려하여 \(y_t\)를 계산합니다.
하지만 입력 시퀀스와 출력 시퀀스의 길이가 다른경우 혹은 단순한 관계가 아닌 경우 일반적인 RNN 구조는 역시 가변길이 시퀀스에 적용할 수 없습니다.
특히 speech recognition, machine translation과 같은 대부분의 NLP task는 이러한 고정된 입, 출력 차원 제약에 맞지 않았습니다.
RNN based Seq2Seq

두개의 RNN을 연결하는 Encoder - Decoder 구조는 가변길이의 입, 출력을 다룰 수 있는 가장 간단한 방법입니다.
$$(x_1,...,x_T)\rightarrow C \rightarrow (y_1,...,y_{T^{'}})$$
encoder-decoder 구조는 \((x_1,...,x_T)\rightarrow C \rightarrow(y_1,...,y_{T^{'}})\)의 순서로
encoder를 통하여 입력 시퀀스 \((x_1,...,x_T)\)를 고정된 길이의 벡터 \(C\)로 표현하고, 다시 decoder를 통하여 고정된 길이의 벡터\(v\)를 출력 시퀀스 \((y_1,...,y_{T^{'}})\)로 매핑하는 구조입니다.
각 입력, 출력 시퀀스의 종료는 보통 <EOS> 토큰을 기준으로 정해집니다.
따라서 encoder- decoder 구조의 입, 출력 길이 \(T\)와 \(T^{'}\)는 <EOS> 토큰의 등장 시기에 따라 달라질 수 있습니다.\((T\neq T^{'})\)
Encoder - Decoder 구조는 일반적인 언어모델(Language model)을 사용하여 다음과 같은 조건부 확률로 모델링 할 수 있습니다.
$$p(y_1,...,y_{T'}|x_1,...,x_T) = \prod_{t=1}^{T'}p(y_t|v,y_1,...,y_{t-1})$$
우변의 \(p(y_t|v,y_1,...,y_{t-1})\)는 모든 vocabulary에 대한 softmax probability로서 표현됩니다.
1. LSTM based Seq2Seq
2014년 발표된 본 논문의 Contribution은 기존 RNN-based seq2seq 모델의 성능을 다음 세가지 방법으로 개선하는 데에 있습니다.
1. LSTM
2. Deep LSTM
3. reversed order Input sequence
1) LSTM
long term dependency는 가장 잘 알려져 있는 RNN의 단점으로, 시퀀스가 길어져 timestep 간의 간격이 멀어질수록 input sequence의 정보를 모델이 제대로 반영하지 못하는 현상을 말합니다.
LSTM과 GRU 구조는 long term dependency 개선하기 위한 가장 대중적인 방법입니다.

첫 번째로 본 논문에서는 Encoder와 Decoder를 각각 LSTM으로 치환하는 방법으로 Seq2Seq 모델의 성능을 개선하였습니다.
LSTM은 선택적으로 hidden state를 삭제, 반영하는 gate function을 사용하여 상대적으로 긴 시퀀스에도 robust한 모습을 보여줍니다.
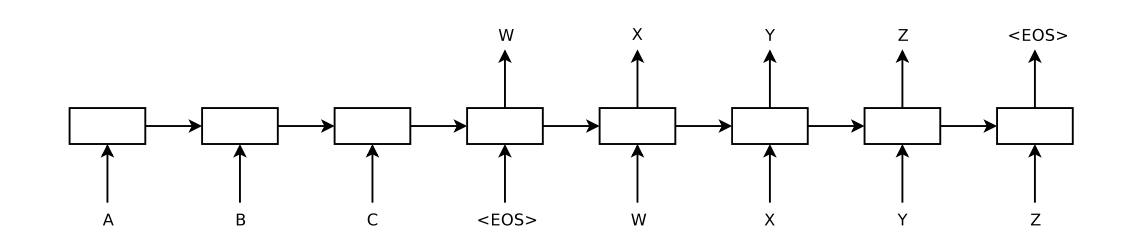
LSTM을 사용한 Seq2Seq 모델의 계산 과정을 위의 예시를 통해 설명드리면,
먼저 LSTM은 입력 시퀀스 (A,B,C,<EOS>)를 차례로 입력받아 고정된 차원의 representation을 계산합니다.
그 후, representation을 입력받은 Decoder는 차례로 softmax probability를 계산하며 출력 시퀀스 (W,X,Y,Z,<EOS>)를 얻게 됩니다.
사실상 메커니즘은 RNN seq2seq 모델과 동일하고, long-term dependency 해결에 주된 목적이 있다고 할 수 있습니다.
2) Deep LSTM
두번째 개선점은 Single layer RNN 구조가 아닌, Deep LSTM을 사용하는 것 입니다.
얕은 구조의 LSTM Encoder, Decoder 구조에 비해 Deep한 구조의 LSTM이 성능을 향상 시켰다고 합니다.
본 논문에서는 4개 층의 LSTM을 사용하였습니다.
3) reversed order Input sequence
세번째 개선점은 reversed order Input sequence를 사용하는 것 입니다.
reversed order Input sequence는 입력 시퀀스의 순서를 거꾸로하여 LSTM encoder의 새로운 입력으로 하는 것 입니다.
간단한 예시를 통해 설명드리면,
\(a,b,c\) 각각에 대응하는 translation이 \(\alpha,\beta,\gamma\)일 때,
$$(a,b,c) \rightarrow (\alpha,\beta,\gamma)$$
$$(c,b,a) \rightarrow (\alpha,\beta,\gamma)$$
위와 같은 형태로 input의 순서를 뒤집는 방법 입니다.
간단한 sequence data의 augmentation 이지만, SGD 최적화 과정이 input, output관계를 더 잘 이해하도록 유도한다고 합니다.
또한 제안하는 방법은 입, 출력간에 서로 대응되는 평균거리는 유지되지만, 최소 거리는 훨씬 줄어들기 때문에 이 또한 긍정적인 영향을 준다고 합니다.
예시의 (\(a,\alpha\))간의 거리가 제안된 방법을 적용한 경우 더 가까워 짐을 알 수 있습니다.
(하지만 최대 거리(\(c, \gamma\))는 늘어납니다. )
objective function
목적함수는 아래와 같이 주어진 문장에 대한 정답 문장의 log likelihood를 최대화 하는 것 입니다.
$$1/|S| \sum_{(T,S)\in S} \log p(T|S)$$
$$\DeclareMathOperator*{\argmax}{argmax}$$
Inference
학습을 마친 후, 번역 등을 생성하는 inference 과정에서는 아래와 같이 가장 큰 확률의 output sequence를 찾는 beam search 과정을 진행합니다.
$$\hat{T} = \argmax_T p(T|S)$$
상위 확률의 B개의 문장 만큼을 beam search를 통해 지속적으로 계산한 후, <EOS> 토큰이 등장하면 해당 문장을 결과 문장으로 사용합니다. Beam size=2 일 때 가장 성능이 좋았으며, Beam size=1을 사용하여도 잘 작동하였다고 합니다.
2.results
실험은 English to French Machine translation 데이터셋을 활용하여 진행되었습니다.
비교 지표로는 BLEU가 사용되었습니다.

BLEU
BLEU(bilingual Evaluation Understudy) score는 input과 output이 모두 sequence로 이루어져 있는 경우 사용하는 지표로서
machine translation task에 주로 사용됩니다.
$$BLEU = min(1,{output\,length(예측\,문장)\over reference\,length(정답\,문장)})(\prod_{i=1}^4precision_i)^{1\over 4}$$
\((\prod_{i=1}^4precision_i)^{1\over 4}\)은 정답 문장과 예측 문장 사이에 n-gram(1~4)이 겹치는 정도의 기하평균 입니다.
이 때, 하나의 단어가 예측문장에 여러번 등장하여 중복계산될 수 있기 때문에, Clipping 작업을 통해 해당단어가 카운팅 되는 횟수는 정답문장에서 등장하는 횟수를 넘지 못하게 합니다.
ex)Clipping
정답문장: "an apple is on the desk"
예측문장: "an an an an apple "
'an'은 정답문장에서 1회 등장 --> 1회 카운팅
before Clipping : 겹치는 횟수 : 5
after Clipping : 겹치는 횟수 : 2
ex)1-gram precision
Clipping 유무에 따른 1-gram precision의 예시입니다.
정답문장: "한화는 10년 안에 우승 할 것이다."
예측문장: "한화는 한화는 한화는 한화는 10년 안에 준우승 할 것이다."
1-gram precision(Clipping X) =\(일치하는\,1-gram\,수\over 모든\,1-gram\,수\) \(=\)\(8\over 9\) 입니다.
1-gram precision(Clipping O) =\(일치하는\,1-gram\,수\over 모든\,1-gram\,수\) \(=\)\(5\over 9\) 입니다.
또한 \(min(1,{output\,length(예측\,문장)\over reference\,length(정답\,문장)})\) term은 문장길이에 대한 과적합을 보정해 줍니다.
비교적 짧은 문장은 결과에 있어 우위를 가져다 줄 수 있기 때문입니다.(Brevity Penalty)
이러한 과정을 통하여 BLEU score가 계산됩니다.
종합하여 볼 때, BLEU는 문장의 길이와 단어의 중복을 고려하여 정답문장과 예측문장 사이의 겹치는 정도를 계산하는 지표라고 생각하면 될 것 같습니다.
result 1.

실험 결과 제안한 방법을 앙상블 한 결과가 baseline 모델에 비해 더 좋은 성능을 보였습니다.
이는 처음으로 neural network를 사용한 모델이 SMT(statistical machine translation) 모델을 능가한 경우라고 합니다.(Table 1)
또한 SMT모델의 상위 1000개 결과를 다시 제안한 방법으로 평가하여 각가 모델의 평균을 결과로 하였을 때, SOTA 모델에 비해서는 약간 모자랐지만 더 향상된 성능을 얻을 수 있었다고 합니다.(Table 2)
result 2.
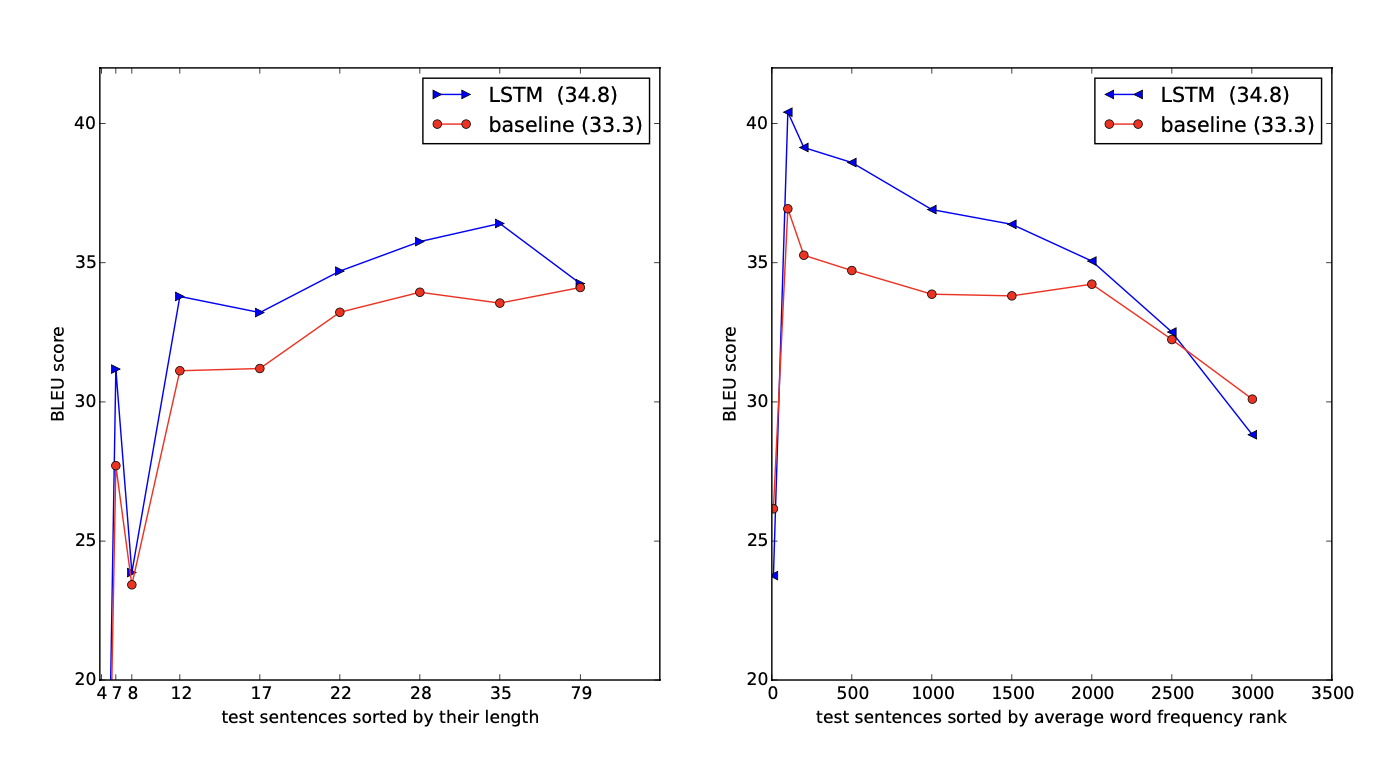
제안한 모델은 충분히 긴 문장에서도 좋은 성능을 보였습니다.
result 3.

제안한 모델의 결과를 PCA를 사용해 2차원 평면에 나타낸 결과입니다.
단어의 순서에 따라서는 민감하지만
문장의 수동,능동 형태에 따라서는 큰 영향을 받지 않았다는 점이 흥미로운 결과였습니다.
마무리
본 논문의 저자들은 RNN기반의 encoder-decoder 구조를 deep LSTM으로 치환하고, reversed order input sequence를 사용하여 long term dependency 문제를 개선하였습니다.
LSTM이 RNN의 long term dependency문제 해결을 위한 한가지 방법임은 당연할 수 있지만,
reversed order input sequence를 사용하는 것은 기발한 아이디어 같습니다.
하지만 실험 단계에서 조금 더 세분화된 비교를 했으면 어땠을까 하는 아쉬움은 있었습니다.
다음으로는 Attention을 사용하는 seq2seq methods에 대하여 리뷰해보도록 하겠습니다.